Der Gini-Koeffizient (Gini-Konzentrationsmaß) ist ein KPI, der die Intensität einer
Ungleichheit (Disparität) darstellt. Er sagt also aus, wie gleich, bzw. ungleich
etwas (z.B. das Einkommen in der Bevölkerung) verteilt ist.
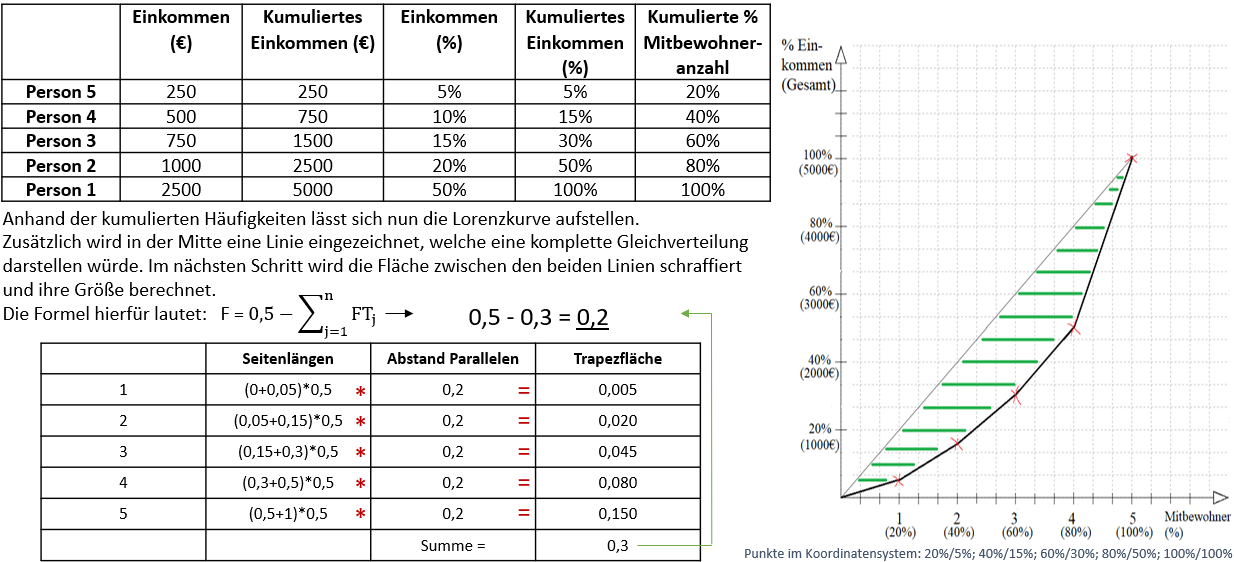
Berechnet wird der Gini-Koeffizient über die Lorenzkurve und er trägt einen Wert zwischen 0 und 1.
Umso größer der Wert des Gini-Koeffizienten ist, desto ungleicher ist die vorhandene Verteilung.

Auch für den Gini-Koeffizienten gibt es verschiedenste Möglichkeiten der Formulierung. Wir behandeln die
allgemeine Definition der Berechnung, welche in den meisten Vorlesungen behandelt wird.